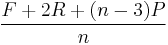Catmull–Clark subdivision surface
The Catmull–Clark algorithm is used in computer graphics to create smooth surfaces by subdivision surface modeling. It was devised by Edwin Catmull and Jim Clark in 1978 as a generalization of bi-cubic uniform B-spline surfaces to arbitrary topology.[1] In 2005, Edwin Catmull received an Academy Award for Technical Achievement together with Tony DeRose and Jos Stam for their invention and application of subdivision surfaces.
Contents |
Recursive evaluation
Catmull–Clark surfaces are defined recursively, using the following refinement scheme:[1]
Start with a mesh of an arbitrary polyhedron. All the vertices in this mesh shall be called original points.
- For each face, add a face point
- Set each face point to be the centroid of all original points for the respective face.
- For each edge, add an edge point.
- Set each edge point to be the average of the two neighbouring face points and its two original endpoints.
- For each face point, add an edge for every edge of the face, connecting the face point to each edge point for the face.
- For each original point P, take the average F of all n face points for faces touching P, and take the average R of all n edge midpoints for edges touching P, where each edge midpoint is the average of its two endpoint vertices. Move each original point to the point
(This is the barycenter of P, R and F with respective weights (n-3), 2 and 1. This arbitrary-looking formula was chosen by Catmull and Clark based on the aesthetic appearance of the resulting surfaces rather than on a mathematical derivation.)
The new mesh will consist only of quadrilaterals, which won't in general be planar. The new mesh will generally look smoother than the old mesh.
Repeated subdivision results in smoother meshes. It can be shown that the limit surface obtained by this refinement process is at least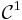 
at extraordinary vertices and 
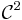everywhere else (when n indicates how many derivatives are continuous, we speak of 
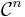continuity). After one iteration, the number of extraordinary points on the surface remains constant.
Exact evaluation
The limit surface of Catmull–Clark subdivision surfaces can also be evaluated directly, without any recursive refinement. This can be accomplished by means of the technique of Jos Stam [2]. This method reformulates the recursive refinement process into a matrix exponential problem, which can be solved directly by means of matrix diagonalization.
Software using Catmull–Clark subdivision surfaces
- 3ds max
- 3D-Coat
- AC3D
- Anim8or
- AutoCAD
- Blender
- Carrara
- CATIA (Imagine and Shape)
- Cheetah3D
- Cinema4D
- DAZ Studio, 2.0
- DeleD Pro
- Gelato
- Hexagon
- Houdini
- JPatch
- K-3D
- LightWave 3D, version 9
- Maya
- Metasequoia
- modo
- Mudbox
- Realsoft3D
- Remo 3D
- Shade
- Silo
- SketchUp -Requires a Plugin.
- Softimage XSI
- Strata 3D CX
- Vue 9
- Wings 3D
- Zbrush
- TopMod
- TopoGun
- [[CREO 1.0 - PTC - (Freestyle)]-]
See also
- Conway polyhedron notation - A set of related topological polyhedron and polygonal mesh operators.
References
- ^ a b E. Catmull and J. Clark: Recursively generated B-spline surfaces on arbitrary topological meshes, Computer-Aided Design 10(6):350-355 (November 1978), (doi, pdf)
- ^ Jos Stam, Exact Evaluation of Catmull–Clark Subdivision Surfaces at Arbitrary Parameter Values, Proceedings of SIGGRAPH'98. In Computer Graphics Proceedings, ACM SIGGRAPH, 1998, 395–404 (pdf, downloadable eigenstructures)